この記事には広告を含む場合があります。
記事内で紹介する商品を購入することで、当サイトに売り上げの一部が還元されることがあります。
くもんの算数に、うちの2人姉妹(小1・年少)がお世話になっている にじまま( @nijimama_m)です。
くもんの算数は、高校数学に必要な計算力を高めることに絞り込んだ教材です。

くもんは弊害のある教材とも言われています。
教材内容を知らずに入会して「弊害だらけだった」ということになりかねません。
弊害と言われている内容をピックアップしてみました。
- 計算問題ばかりで「考える力」が身につかない
- 学校で習う範囲をカバーしてくれていない
- 先取りすることだけに集中してしまいがち

実は、弊害と言われていことにもちゃんと理由があります。
理由に納得できれば弊害ではないし、違うなと思えば弊害になります。
この記事では、くもんの算数教材がどんなものかを個人的な感情を入れずに紹介しています。
記事の内容を読んで、公文式が教育方針と合っているかどうか、判断基準にしてもらえたらと思います。
くもんの算数は 高校数学に必要な代数計算力を高めることに絞り込んだ教材です。

微分・積分や難しい方程式を自力で解けるようになるための教材ということです。
数学ができない子は、文字を使った計算が弱いという統計が公文式にあります。
文字を使った計算とは、aやb、xやyなどを使った計算、つまり代数計算のことです。
この代数計算がスラスラできるかどうかが、算数・数学ができるかできないかを決めます。
中学では、一次方程式、因数分解。
高校からは、二次関数、指数関数、三角関数、微分・積分、ベクトル、確率など、ほとんどの内容が代数計算です。
代数計算を解くには、基礎である たし算・ひき算・かけ算・わり算・分数や正負の計算の力が必要です。
複雑な代数計算を解くためには、基礎的な計算を速く正確に解くことが不可欠ということです。
図形や文章問題がない理由
くもんは、高校数学に必要な代数計算力を高めることに絞り込んだ教材です。

そのため、算数教材は計算問題ばかりです。
「図形や文章問題、応用問題もあればいいのに」という意見も多いそうです。

図形や文章問題がないことについての公文の回答がこちらです。
図形について
自分の学年より2年分、3年分・・と先の教材に進んだ子は、学年相当の図形問題ならすぐできる。
文章問題について
文章問題ができない理由は、計算力が十分でない、もしくは問題の意味がくみ取れていない。
問題の意味がくみ取れていないなら、国語力を鍛えることが必要。
- まずは計算力を高めることが大切
- 文章問題を読み取る力「国語力」を身につける
計算で数学的思考を高める
公文の算数は、計算の手順を子ども自身に気づかせるように作られています。
子どもが自分で計算の仕方、計算の道筋に気づけるような問題構成です。

中学や高校の数学では、どこから解くべきか、どの手順が効率いいか、計算の道筋を立てて理論的に考える力が必要となります。
そして、これでいいか検証したり分析したりする力も必要です。
公文式は、たくさん計算練習することで数学的センスを高めたいと考えています。
くもんと言えば、反復練習です。
どのくらい練習するのかは「標準完成時間」を基準に判断されます。

1枚につき2〜4分で仕上げる、といった時間設定がされています。
年齢や学年に関係なく、実際のプリント学習にかかった時間と「標準完成時間」を照らし合わせて判断されます。
「正確さ」と「時間」で判断されます。
6A・5A・4A・3A・2A教材
くもんの算数は、数の理解・数の読み書きができるようになる教材からはじまります。
数字を読んだり書いたりしたことのない子どもでも、学習をはじめることができます。


3A教材で、120までの数の読み書きを練習していきます。
数を読んだり書いたりできるようになると、数が理解できるようになります。
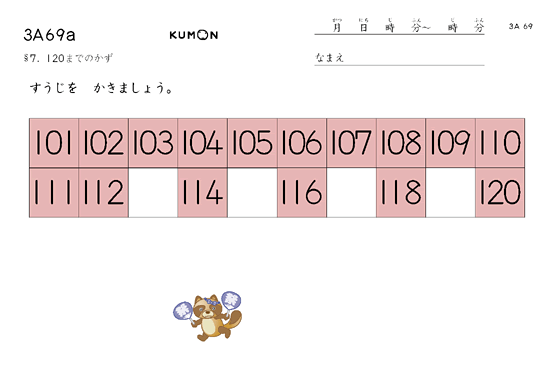
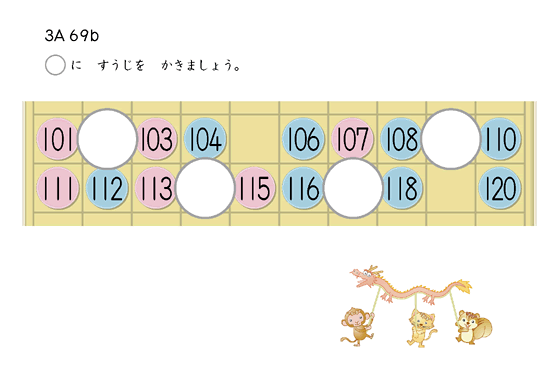
120までの読み書きができたら、たし算です。
くもんのたし算は「たす1」をくり返します。
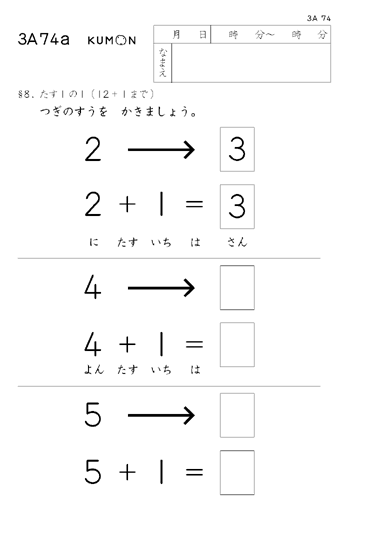
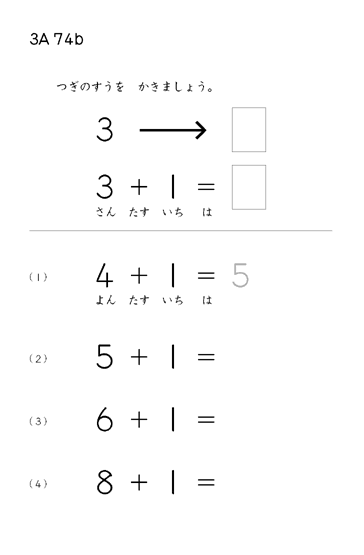
120までの読み書きがしっかりできていれば幼児でも、5の次は6、9の次は10がすっと理解できます。
この「たす1」を何度もくり返すことで、その次の数として「たす2」、「たす3」・・と学んでいきます。
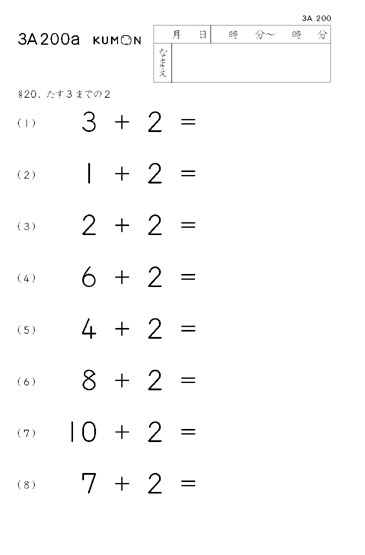

小さい子どもは特に前に学習したことを使って次の段階に進むと、新しい内容を習得しやすくなります。
 【公文式】3A・2Aの足し算がぜんぜん進まない子どもへの教え方
【公文式】3A・2Aの足し算がぜんぜん進まない子どもへの教え方
A・B・C教材
A教材では「12+6」「18+8」など、2ケタを含む計算がスラスラできるようになってから、ひき算に進みます。


たし算がしっかりできていれば、ひき算はらくらく進むことができます。
B教材ではたし算・ひき算の筆算、
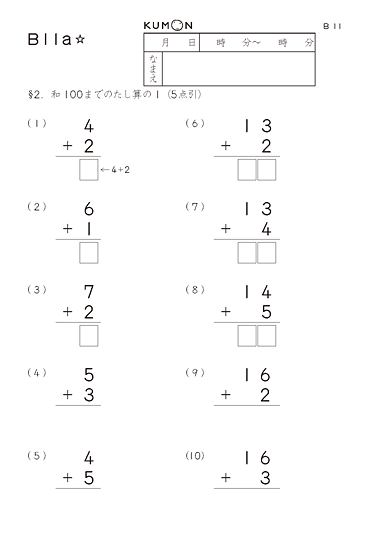

C教材ではかけ算・わり算を練習します。


くもんの特徴として、くり上がりやくりさがりの計算をするとき、くり上がる数を忘れないようにする書き留めをさせません。
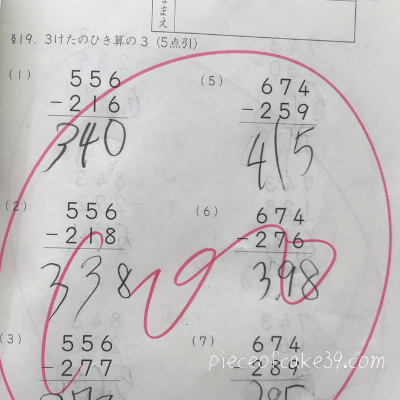
わり算の筆算、「2ケタ÷1ケタ」「3ケタ÷1ケタ」も、下に書かずに計算するよう、指導されます。

理由は、暗算力を高めたいからです。
これから難しくなっていく計算問題では、頭の中で素速く、たし算・ひき算・かけ算・わり算をする力が必要です。
暗算する力を身につけるため、素速く正確に計算できるように練習します。
D・E・F教材
D教材から分数がはじまります。

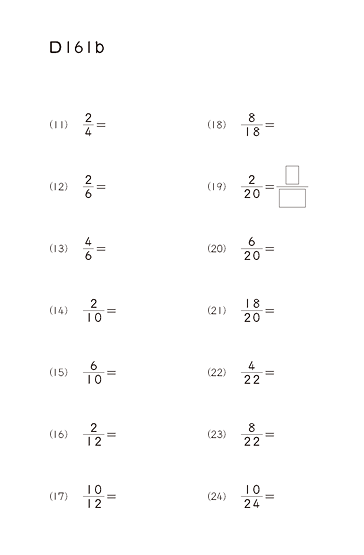
初めての分数にもかかわらず、例題を見て答える構成になっています。
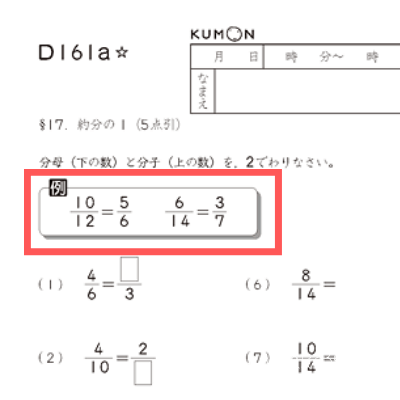
分数とは何か、例えばピザを8等分したときの1つが8分の1・・というような説明がありません。

理由は、子どもは ことばや図で説明されても、かえって理解できない場合が多いからです。
まず例題を見て、なぜ「5分の20」が「4」になるんだろう?と自分で考えることが大切としています。

E教材、F教材では、分数のたし算・ひき算・かけ算・わり算、複雑な四則混合の分数を学習します。
公文式では、あまり教科書でとりあげられていない帯分数を含んだ分数計算を重視しています。
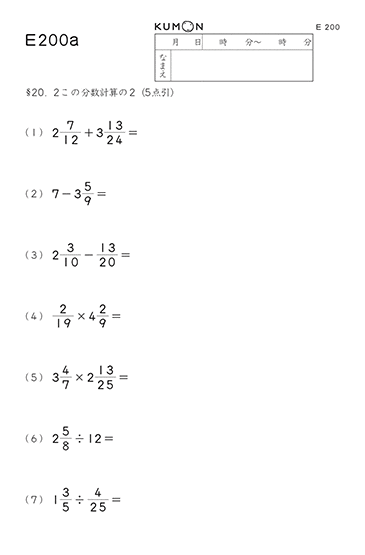

帯分数とは、整数と真分数の和をまとめた形で書いたものです。

帯分数を含んだ分数計算を重視している理由は2つです。
- 高いレベルの計算力が身につく
- 順序立てて考える力や処理する力を高めるため
この2つは、中学や高校での複雑な代数計算を解いていくのに欠かせないものです。
G・H・I教材:中学数学の力をつける
G教材からは、中学数学です。
一次方程式で検算の習慣を身につけていきます。


検算とは、計算をしたあとで、間違いがないかどうか確かめるため、もう一度計算してみることです。
H教材では二次方程式に加えて、中学では習わない「三元・四元連立方程式」を練習します。


なぜ中学では習わない「三元・四元連立方程式」まで練習するのでしょうか。
理由は、高校数学で二次関数、図形と方程式など、三元以上の連立方程式を必要となる勉強があるからです。
公文式算数は、どこまでも高校数学をスラスラ解けるようになることにあります。
中学レベルの教材は、例題を見てやり方を自分でつかみ、解いていくようになっていきます。
自分の力で解き方や考え方を身につけ、自習力を高めていきます。
J・K・L・M・N・O・P教材:高校数学の力をつける
J教材から、公文式算数・数学教材の目標である高校教材に入ります。
J教材では「因数分解」「無理数」「虚数(きょすう)」「判別式」「因数定理」などを学習します。


K教材では「二次関数」「高次関数」「無理関数」「指数関数」などを学習。
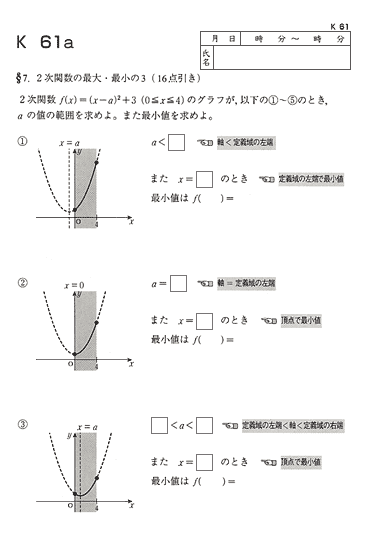
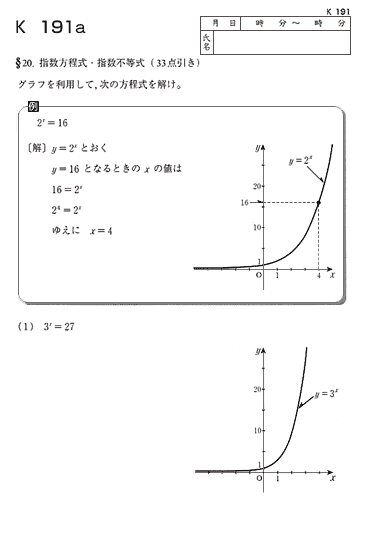
関数とグラフに対する感覚を高め、微分・積分にそなえます。
そして、いよいよL教材。
二次関数や三次関数の微分・積分を学びます。


ここまでが高校数学の基礎内容です。
M〜P教材は、広範囲な高校数学の単元をひととおり学習します。
P教材が数学の最終教材となります。
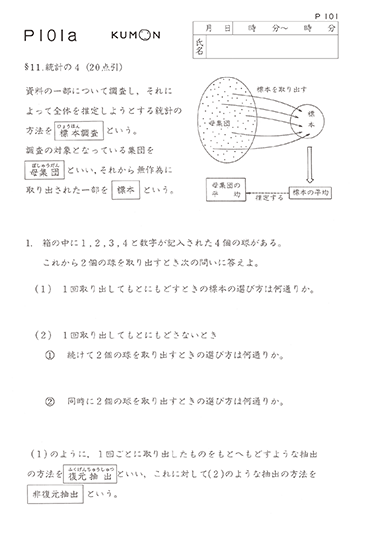

もっと公文式算数で学びたい人には、高校算数の領域を超えた「研究コース」があります。
この記事では、くもんの算数ってどんな教材?弊害があるって本当?について書きました。
公文式算数は、高校数学に必要な代数計算力を高めることに絞り込んだ教材です。
ここを知らずに入会すると、「考える力」が身につかない、学校で習う範囲をカバーしてくれていないという、弊害だらけになってしまいます。

教育方針と公文式が合いそうか、この記事を参考に判断してみてください。
最後まで読んでいただき、ありがとうございました。
にじますでした。


